With an exact recursive approach, we study photonic crystal fibers and resonators with topological features induced by Aubry–Andre–Harper cladding modulation. We find nontrivial gaps and edge states at the interface between regions with different topological invariants. These structures show topological protection against symmetry-preserving local perturbations that do not close the gap and sustain strong field localization and energy concentration at a given radial distance. As topological light guiding and trapping devices, they may bring about many opportunities for both fundamentals and applications unachievable with conventional devices.
Category: PRIN 2015 NEMO
Controlling rogue waves and soliton gases
Topological control of extreme waves
From optics to hydrodynamics, shock and rogue waves are widespread. Although they appear as distinct phenomena, transitions between extreme waves are allowed. However, these have never been experimentally observed because control strategies are still missing. We introduce the new concept of topological control based on the one-to-one correspondence between the number of wave packet oscillating phases and the genus of toroidal surfaces associated with the nonlinear Schrödinger equation solutions through Riemann theta functions. We demonstrate the concept experimentally by reporting observations of supervised transitions between waves with different genera. Considering the box problem in a focusing photorefractive medium, we tailor the time-dependent nonlinearity and dispersion to explore each region in the state diagram of the nonlinear wave propagation. Our result is the first realization of topological control of nonlinear waves. This new technique casts light on shock and rogue waves generation and can be extended to other nonlinear phenomena.
Nature Communications volume 10, Article number: 5090 (2019)
Optical spatial shock waves in nonlocal nonlinear media, a review paper
Dispersive shock waves are fascinating phenomena occurring when nonlinearity overwhelms linear effects, such as dispersion and diffraction. Many features of shock waves are still under investigation, as the interplay with noninstantaneity in temporal pulses transmission and nonlocality in spatial beams propagation. Despite the rich and vast literature on nonlinear waves in optical Kerr media, spatial dispersive shock waves in nonlocal materials deserve further attention for their unconventional properties. Indeed, they have been investigated in colloidal matter, chemical physics and biophotonics, for sensing and control of extreme phenomena. Here we review the last developed theoretical models and recent optical experiments on spatial dispersive shock waves in nonlocal media. Moreover, we discuss observations in novel versatile materials relevant for soft matter and biology.
Topology into the Ring: new fibers and resonators
Topological photonic crystal fibers and ring resonators
We study photonic crystal fibers and ring resonators with topological features induced by Aubry- Andre-Harper modulations of the cladding. We find non-trivial gaps and edge states at the interface between regions with different Chern numbers. We calculate the field profile and eigenvalue dispersion by an exact recursive approach. Compared with conventional circular resonators and fibers, the proposed structure features topological protection and hence robustness against symmetry-preserving local perturbations that do not close the gap. These topological photonic crystal fibers sustain strong field localization and energy concentration at a given radial distance. As topological light guiding and trapping devices, they may bring about many opportunities for both fundamentals and applications unachievable with conventional optical devices.
Laura Pilozzi, Daniel Leykam, Zhigang Chen, Claudio Conti in ArXiv:1909.02081
See also
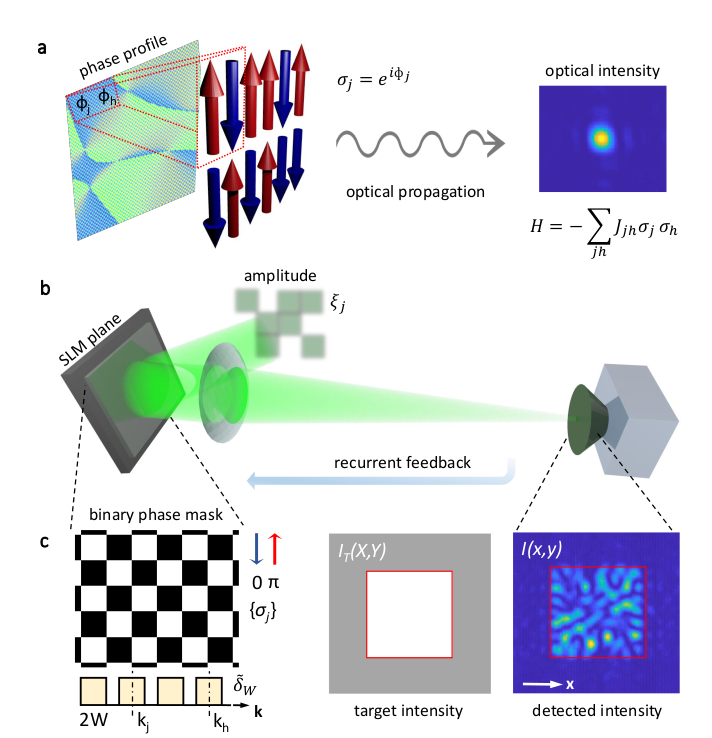
Super-Duper Ising Machine by a Single SLM
Quantum and classical physics can be used for mathematical computations that are hard to tackle by conventional electronics. Very recently, optical Ising machines have been demonstrated for computing the minima of spin Hamiltonians, paving the way to new ultra-fast hardware for machine learning. However, the proposed systems are either tricky to scale or involve a limited number of spins. We design and experimentally demonstrate a large-scale optical Ising machine based on a simple setup with a spatial light modulator. By encoding the spin variables in a binary phase modulation of the field, we show that light propagation can be tailored to minimize an Ising Hamiltonian with spin couplings set by input amplitude modulation and a feedback scheme. We realize configurations with thousands of spins that settle in the ground state in a low-temperature ferromagnetic-like phase with all-to-all and tunable pairwise interactions. Our results open the route to classical and quantum photonic Ising machines that exploit light spatial degrees of freedom for parallel processing of a vast number of spins with programmable couplings.
D. Pierangeli, G. Marcucci, C. Conti in ArXiv:1905.11548 and Phys. Rev. Lett. 122, 213902 (2019)
See also