We investigate the dynamics of multi-mode optical systems driven by two-photon processes and subject to non-local losses, incorporating quantum noise at the Gaussian level. Our findings show that the statistics from a single Gaussian quantum trajectory exhibit emergent thermal equilibrium governed by an Ising Hamiltonian encoded in the dissipative coupling between modes. The driving strength sets the system’s effective temperature relative to the oscillation threshold. Given the ultra-short time scales typical of all-optical devices, our study demonstrates that such multi-mode optical systems can operate as ultra-fast Boltzmann samplers, paving the way toward the realization of efficient hardware for combinatorial optimization, with promising applications in machine learning and beyond.
Category: Nonlinear Physics
Quantum Hyperspins: A New Schroedinger’s Cat ?
https://arxiv.org/abs/2411.05728
We report on the emergence of a highly non-classical collective behavior in quantum parametric oscillators, which we name quantum hyperspin, induced by a tailored nonlinear interaction. This is the second quantized version of classical multidimensional spherical spins, as XY spins in two dimensions and Heisenberg spins in three dimensions. In the phase space, the quantum hyperspins are represented as spherical shells whose radius scales with the number of particles in a way such that it cannot be factorized even in the limit of large particle number. We show that the nonlinearly coupled quantum oscillators form a high-dimensional entangled state that is surprisingly robust with respect to the coupling with the environment. Such a behavior results from a properly engineered reservoir. Networks of entangled quantum hyperspins are a new approach to quantum simulations for applications in computing, Ising machines, and high-energy physics models. From first principles through ab initio numerical simulations, we analyze the properties of quantum hyperspins, including the interplay of entanglement and coupling frustration.
Observation of 2D dam break flow and a gaseous phase of solitons in a photon fluid in PRL
We report the observation of a two-dimensional dam break flow of a photon fluid in a nonlinear optical crystal. By precisely shaping the amplitude and phase of the input wave, we investigate the transition from one-dimensional (1D) to two-dimensional (2D) nonlinear dynamics. We observe wave breaking in both transverse spatial dimensions with characteristic timescales determined by the aspect ratio of the input box-shaped field. The interaction of dispersive shock waves propagating in orthogonal directions gives rise to a 2D ensemble of solitons. Depending on the box size, we report the evidence of a dynamic phase characterized by a constant number of solitons, resembling a 1D solitons gas in integrable systems. We measure the statistical features of this gaseous-like phase. Our findings pave the way to the investigation of collective solitonic phenomena in two dimensions, demonstrating that the loss of integrability does not disrupt the dominant phenomenology.
https://arxiv.org/abs/2409.18738
https://mathstodon.xyz/@nonlinearxwaves/113258813170717367
https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.133.183801
Non-Gaussianity in the quantum parametric oscillator
https://journals.aps.org/pra/abstract/10.1103/PhysRevA.109.063519
Systems of coupled optical parametric oscillators (OPOs) forming an Ising machine are emerging as large-scale simulators of the Ising model. The advances in computer science and nonlinear optics have triggered not only the physical realization of hybrid (electrooptical) or all-optical Ising machines, but also the demonstration of quantum-inspired algorithms boosting their performances. To date, the use of the quantum nature of parametrically generated light as a further resource for computation represents a major open issue. A key quantum feature is the non-Gaussian character of the system state across the oscillation threshold. In this paper, we perform an ab initio analysis of the emergence of non-Gaussianity in the single quantum OPO with an applied external field. We model the OPO by a Lindblad master equation, which is numerically solved by a first-principles method based on exact diagonalization. Non-Gaussianity is quantified by means of three different metrics: the Hilbert-Schmidt distance, quantum relative entropy, and photon distribution. Our findings reveal a nontrivial interplay between parametric drive and applied field: (i) the increasing pump monotonically enhances non-Gaussianity and (ii) the increasing field first sharpens non-Gaussianity, and then restores the Gaussian character of the state when above a threshold value. We also report a first-principles computation in the Fock space of the distance from the mixture of coherent states, a strongly nonclassical behavior that can play a significant role in the quantum parallel search for optimization.
See also arXiv
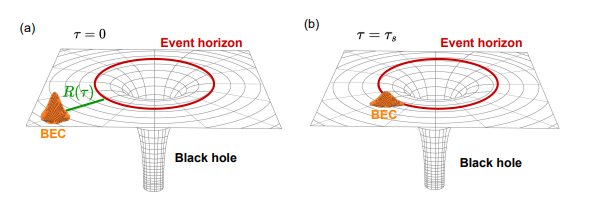
Non local solitons and dark matter in NJP !
Theories on the bosonic nature of dark matter are a promising alternative to the cold dark matter model. Here we consider a dark matter halo in the state of a Bose–Einstein condensate (BEC), subject to the gravitation of a black hole. In the low energy limit, we bring together the general relativity in the Schwarzschild metric and the quantum description of the BEC. The model is solvable in the Fermi normal coordinates with the so-called highly nonlocal approximation and describes tidal deformations in the condensate wave function. The black hole deforms the localized condensate until the attraction of the compact object overcomes the self-gravitation and destabilizes the solitonic dark matter. Moreover, the model can be implemented as a gravitational analog in the laboratory; the time-dependent potential generated by the galactic black hole can be mimicked by an optical trap acting on a conventional condensate. The results open the way to new laboratory simulators for quantum gravitational effects.