Polarization images offer crucial functionalities across multiple scientific domains, providing access to physical information beyond conventional measures such as intensity, phase, and spectrum of light. However, the challenge of transmitting polarization images through complex media has restricted their application in optical communication and imaging. Here, a novel approach utilizing deep learning for the transmission of full-Stokes polarization images through scattering media is presented. It is demonstrated that any input polarization image can be reconstructed in a single shot by employing only an intensity sensor. By supervised training of a deep neural network, high-accuracy full-Stokes reconstruction is achieved from the speckle pattern detected by an intensity camera. Leveraging the deep learning based polarization decoder, a polarization-colored encoding scheme is devised to enable increased-capacity data transmission through disordered channels. Fast, wavelength-independent, on-chip, polarization imaging in complex media enables the utilization of polarization-structured light in multimode fibres and opaque materials, unlocking new possibilities in optical communication, cryptography, and quantum technology.
Category: Data-driven Physics
Non-Gaussianity in the quantum parametric oscillator
https://journals.aps.org/pra/abstract/10.1103/PhysRevA.109.063519
Systems of coupled optical parametric oscillators (OPOs) forming an Ising machine are emerging as large-scale simulators of the Ising model. The advances in computer science and nonlinear optics have triggered not only the physical realization of hybrid (electrooptical) or all-optical Ising machines, but also the demonstration of quantum-inspired algorithms boosting their performances. To date, the use of the quantum nature of parametrically generated light as a further resource for computation represents a major open issue. A key quantum feature is the non-Gaussian character of the system state across the oscillation threshold. In this paper, we perform an ab initio analysis of the emergence of non-Gaussianity in the single quantum OPO with an applied external field. We model the OPO by a Lindblad master equation, which is numerically solved by a first-principles method based on exact diagonalization. Non-Gaussianity is quantified by means of three different metrics: the Hilbert-Schmidt distance, quantum relative entropy, and photon distribution. Our findings reveal a nontrivial interplay between parametric drive and applied field: (i) the increasing pump monotonically enhances non-Gaussianity and (ii) the increasing field first sharpens non-Gaussianity, and then restores the Gaussian character of the state when above a threshold value. We also report a first-principles computation in the Fock space of the distance from the mixture of coherent states, a strongly nonclassical behavior that can play a significant role in the quantum parallel search for optimization.
See also arXiv
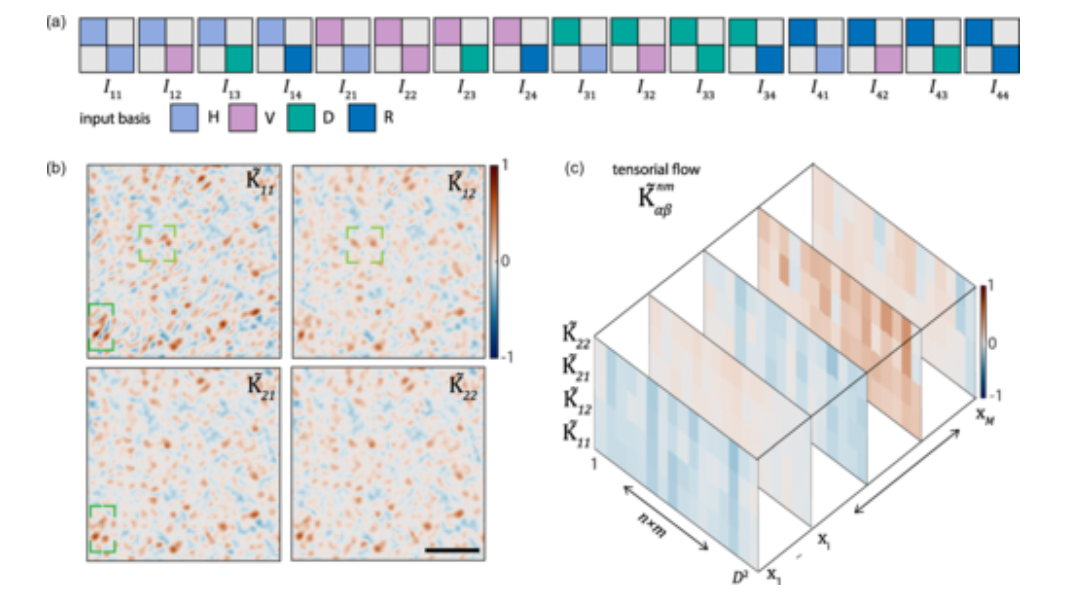
Tensorial flow of mosaic beams in PRL !
https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.132.243801
Optical beams with nonuniform polarization offer enhanced capabilities for information transmission, boasting increased capacity, security, and resilience. These beams possess vectorial features that are spatially organized within localized three-dimensional regions, forming tensors that can be harnessed across a spectrum of applications spanning quantum physics, imaging, and machine learning. However, when subjected to the effect of the transmission channel, the tensorial propagation leads to a loss of data integrity due to the entanglement of spatial and polarization degrees of freedom. The challenge of quantifying this spatial-polarization coupling poses a significant obstacle to the utilization of vector beams in turbulent environments, multimode fibers, and disordered media. Here, we introduce and experimentally investigate mosaic vector beams, which consist of localized polarization tesserae that propagate in parallel, demonstrating accurate measurement of their behavior as they traverse strongly disordered channels and decoding their polarization structure in single-shot experiments. The resultant transmission tensor empowers polarization-based optical communication and imaging in complex media. These findings also hold promise for photonic machine learning, where the engineering of tensorial flow can enable optical computing with high throughput.
Terahertz imaging super-resolution for documental heritage diagnostics
https://ieeexplore.ieee.org/document/10551541
Terahertz imaging provides valuable insights into the composition and structure of objects or materials, with applications spanning security screening, medical imaging, materials science, and cultural heritage preservation. Despite its widespread utility, traditional terahertz imaging is limited in spatial resolution to approximately 1 mm according to Abbe’s formula. In this paper, we propose a novel super-resolution method for terahertz time-domain spectroscopy systems. Our approach involves spatial filtering through scattering in the far-field of high spatial frequency components of the imaged sample. This method leverages evanescent wave filtering using a knife edge, akin to a standard structured illumination scheme. We demonstrate improved spatial resolution in slit diffraction, edge imaging, and reflection imaging of structures fabricated on a paper substrate using commonly encountered materials in works of art and documents. Furthermore, we present super-resolved images of an ancient document on parchment, showcasing the effectiveness of our proposed method.
Efficient Computation Using Spatial-Photonic Ising Machines: Utilizing Low-Rank and Circulant Matrix Constraints
https://arxiv.org/abs/2406.01400
We explore the potential of spatial-photonic Ising machines (SPIMs) to address computationally intensive Ising problems that employ low-rank and circulant coupling matrices. Our results indicate that the performance of SPIMs is critically affected by the rank and precision of the coupling matrices. By developing and assessing advanced decomposition techniques, we expand the range of problems SPIMs can solve, overcoming the limitations of traditional Mattis-type matrices. Our approach accommodates a diverse array of coupling matrices, including those with inherently low ranks, applicable to complex NP-complete problems. We explore the practical benefits of low-rank approximation in optimization tasks, particularly in financial optimization, to demonstrate the real-world applications of SPIMs. Finally, we evaluate the computational limitations imposed by SPIM hardware precision and suggest strategies to optimize the performance of these systems within these constraints.