Observation of Lump Solitons — after 50 years
https://doi.org/10.1103/ggbs-y21w
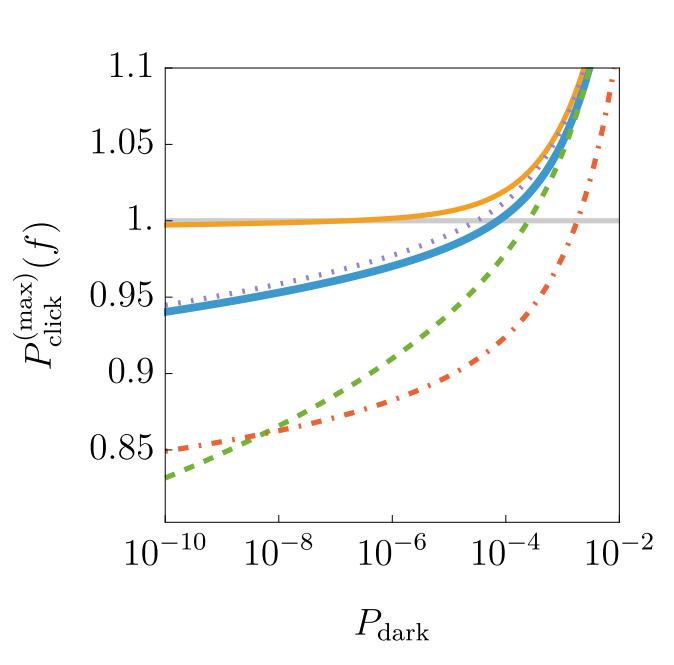
Solitons are the cornerstone of nonlinear physics. The integrability of nonlinear equations is the basis of this universal concept. However, most multidimensional systems lack integrability, a fundamental limitation that challenges the existence of solitons in high dimensions. A remarkable exception would be the lump soliton, a two-dimensional solution of the Kadomtsev-Petviashvili (KP) equation with the unique property of propagating unperturbed in three-dimensional space. Due to the difficulty of implementing the KP dynamics in any physical system, lump solitons have never been observed. Here, we report the first experimental observation of the lump soliton. The lump is realized in nonlinear optics, in a photorefractive crystal under the action of paraxial diffraction and defocusing nonlinearity, ruled by the (2+1)D nonlinear Schrödinger (NLS) equation. We tailor the input field shape and the nonlinearity to realize the hydrodynamic KP integrable regime of the NLS equation. The lump emerges as a self-localized wave that propagates unaltered with a transverse velocity. We confirm its integrable nature by reporting, for the first time, the elastic collision of lumps in two dimensions. As the first experimental evidence of integrable solitons in high dimensions, our observation paves the way for a new era in the study of nonlinear systems.
Featured in Physics, Editors’suggestion
https://physics.aps.org/articles/v19/s22
https://phys.org/news/2026-01-physicists-resilient-3d-solitons-lab.html
Realistic prospects for testing a relativistic local quantum measurement inequality
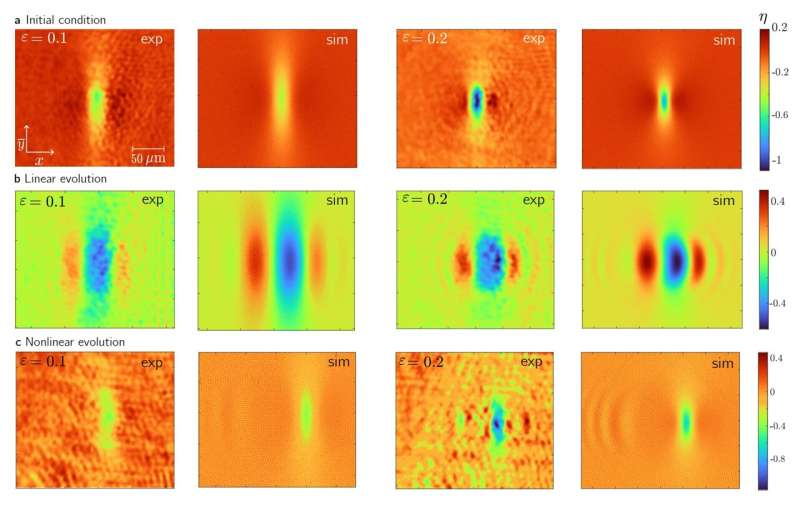
We investigate the experimental prospects for testing a relativistic local quantum measurement inequality that quantifies the trade-off between vacuum insensitivity and responsiveness to excitations for finite-size detectors. Building on the Reeh–Schlieder approximation for coherent states, we derive an explicit and practically applicable bound for arbitrary coherent states. To connect with realistic photodetection scenarios, we model the detection region as a square prism operating over a finite time window and consider a normally incident single-mode coherent state. Numerical results exhibit the expected qualitative behavior: suppressing dark counts necessarily tightens the achievable click probability.
An inequality for relativistic local quantum measurements
We investigate the trade-off between vacuum insensitivity and sensitivity to excitations in finite-size detectors, taking measurement locality as a fundamental constraint. We derive an upper bound on the detectability of vacuum excitation, given a small but nonzero probability of false positives in the vacuum state. The result is independent of the specific details of the measurement or the underlying physical mechanisms of the detector and relies only on the assumption of locality. Experimental confirmation or violation of the inequality would provide a test of the axioms of algebraic quantum field theory, offer new insights into the measurement problem in relativistic quantum physics, and establish a fundamental technological limit in local particle detection.
Reeh-Schlieder approximation for coherent states
We present an explicit, fully local Reeh-Schlieder approximation scheme for coherent states of a free scalar field. For any bounded region U, we construct a one-parameter family of bounded operators A^ζ localized in the causal complement of U. The action of A^ζ on the vacuum approximates the target coherent state in the limit ζ→0.